Loss Function in Machine Learning
This post introduces some basic loss functions used in machine learning training task, mostly in neural nets
In machine learning, we feed a model is to feed it with some data, and get the predicted output. How do we know that the output is good enough? For human, this is easy. However, for a machine, we need to explicitly tell it by quantitative measures and force it to correct the mistakes. Those quantitative measures are loss functions, and there are so many of them. In this post, I will introduce some commonly-used ones and the intuition behind them. I will use pytorch as code examples.
- Mean Square Error Loss
torch.nn.MSELoss
It measures the mean sqaured error, or \(L_2\) norm
\[Loss(x,y) = (x-y)^2\]where x is predicted value and y is ground-truth.
The sqaure here means that we kind of want to punish more on large mistakes. In fact, when we are talking about \(L_k\) norm, the larger the k, the more we want to encourage small mistakes.
Use case:
- regression problems
- Negative Log-Likelihood Loss
torch.nn.NLLLoss
It maximizes the overall probability of the data and penalizes the model with low predicted probability for correct labels and encourages high predicted probability for correct labels. We take negative because the probability is in the range \([0, 1]\) and logrithm in this range is negative. So we turn it into postive by taking a negative.
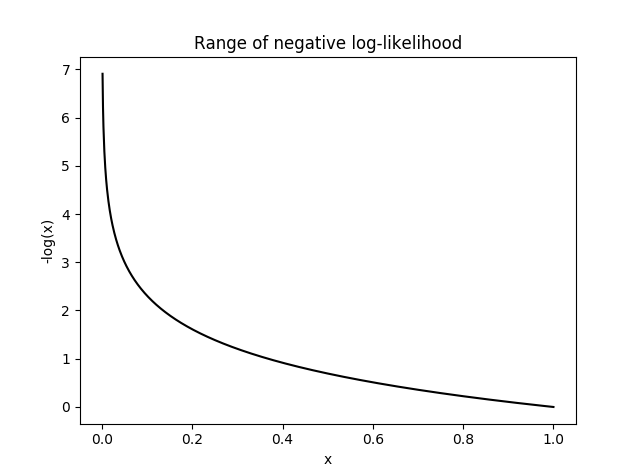
Let’s take a very simple example. For this three-class classification problem, the model predicts the horse (correct label) to be \(98%\), meaning that it did a pretty good job. Thus, we don’t want to penalize the model too much by attaching it a loss of 0.02. This is a very low value. However, the model predicts dog with a so-so confidence so we want to penalize the model with a bit higher loss.
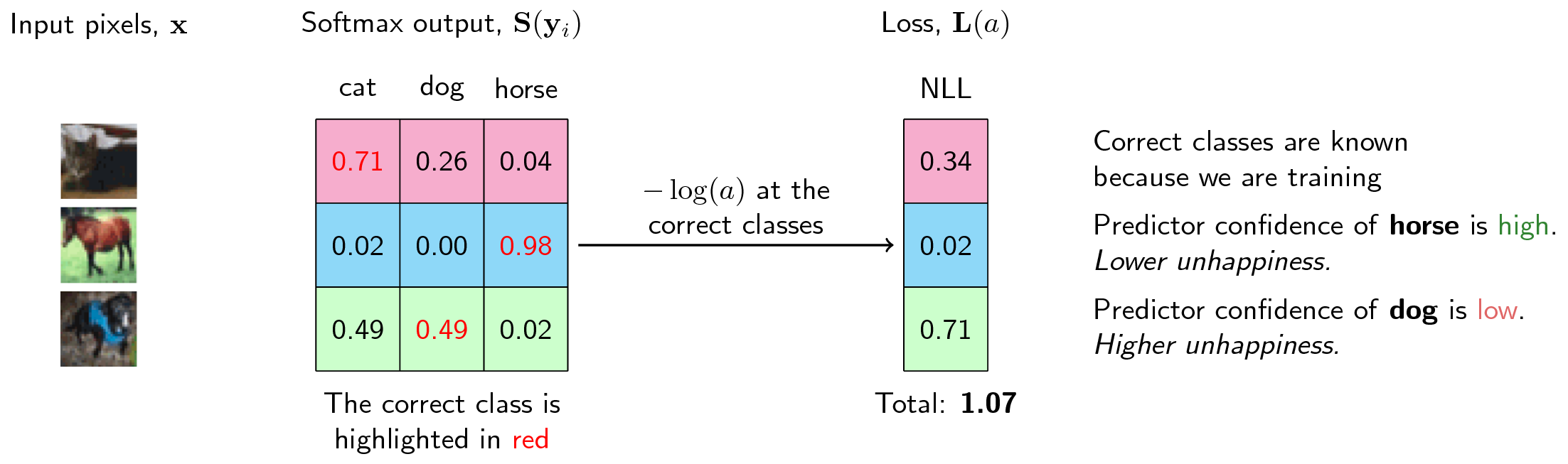
In practice, the negative log-likelihood (NLL) is used in tandem with softmax activation function. It is fairly easy to understand why. As I mentioned above, the input of NLL is a probability. Luckily, softmax function outputs an array of probability according to each class, which is a perfect input for NLL.
Of course, for convinience, torch.nn.functional has a function that combines softmax and negative log-likelihood called torch.nn.functional.cross_entropy
Cross-Entropy Loss
torch.nn.CrossEntropyLoss
It measures the cross-entropy between the predicted and the actual value.
\[Loss(x,y) = - \sum xlog(y)\]where x is the probability of true label and y is the probability of predicted label.
Cross-entropy as a loss function is used to learn the probability distribution of the data. While other loss functions like squared loss penalize wrong predictions, cross entropy gives a greater penalty when incorrect predictions are predicted with high confidence. What differentiates it with negative log loss is that cross entropy also penalizes wrong but confident predictions and correct but less confident predictions, while negative log loss does not penalize according to the confidence of predictions.
Kullback-Leibler divergence
torch.nn.KLDivLoss
KL divergence gives a measure of how two probability distributions are different from each other.
\[Loss(x,y) = y \cdot (\text{log }y - x)\]where x is the probability of true label and y is the probability of predicted label.
It is quite similar to cross entropy loss. The distinction is the difference between predicted and actual probability. This adds data about information loss in the model training. The farther away the predicted probability distribution is from the true probability distribution, greater is the loss. It does not penalize the model based on the confidence of prediction, as in cross entropy loss, but how different is the prediction from ground truth. It usually outperforms mean square error, especially when data is not normally distributed. The reason why cross entropy is more widely used is that it can be broken down as a function of cross entropy. Minimizing the cross-entropy is the same as minimizing KL divergence: KL = Entropy — Cross-entropy